Как ранее говорилось, при поворотно-зеркальной симметрии, объект должен обладать как поворотной, так и зеркальной симметрией. Для описания симметрии конкретного объекта надо указать все поворотные оси и их порядок, а также все плоскости зеркальной симметрии.

Ниже приведены примеры двухмерных объектов с поворотными осями разного порядка и с осями зеркальной симметрии.

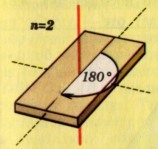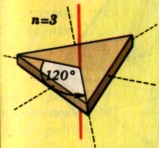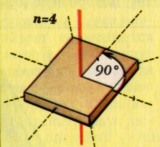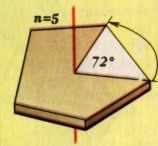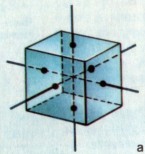
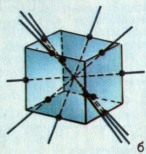
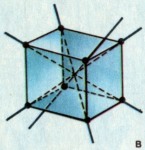
У трёхмерного объекта может быть несколько поворотных осей. Рассмотрим куб. Легко сообразить, что он имеет три поворотные оси 4-го порядка. (рис.а) При более внимательном рассмотрении обнаруживаются 6 поворотных осей 2-го порядка, проходящих через середины противоположных параллельных рёбер (рис.б), а так же четыре поворотные оси 3-го порядка, совпадающие с внутренними диагоналями куба (рис.в). Таким образом, куб имеет всего 13 поворотных осей, среди которых встречаются оси 2-го, 3-го и 4-го порядка. Наряду с поворотными осями, куб имеет и 9 плоскостей зеркальной симметрии.

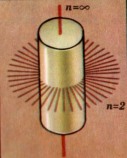Интересна поворотная симметрия кругового цилиндра. Он имеет бесконечное число поворотных осей 2-го порядка и одну поворотную ось бесконечно высокого порядка. Бесконечное число осей симметрии имеют так же круг, щар, круговой конус, элипсоид вращения.